Introduction
The test automation isn't done just for fun. It has the purpose. Some of the main purposes are:
- Increase testing team capacity
- Minimize testing cycle without changing testing team capacity
- Increase testing coverage without extra resources
- Minimize human factor
But all above and many other benefits can be expressed with the single phase.
Test automation should bring the profit. In other words, I have many ways to improve the testing efforts and each of them require some investment. Either I can hire more people or I can invest into some software/hardware which helps me making things faster. But if the investment into some improvement doesn't bring the profit this investment is useless. This is related to test automation as well. Yes, you can buy some expensive tools, you can build the complex infrastructure but if I can do the same in some other way which requires less investment I'll prefer the second option. So, before proposing some test automation efforts we should realize what the advantage we should make with this. One of the wide spread measure is the
Return of investment. So, how should we calculate that for test automation project? Let's build some process model to see what we can calculate there.
What should we measure
First of all, we should identify what the return of investment is.
According to Investopedia:
|
A performance measure used to evaluate the efficiency of an investment or to compare the efficiency of a number of different investments. To calculate ROI, the benefit (return) of an investment is divided by the cost of the investment; the result is expressed as a percentage or a ratio.
|
In other words we pay something with an expectation to gain something. So, return of investment is the ratio between the clean profit and total investment. If this ratio is positive the investment is profitable. Another thing is that when we expect that profit to happen. That's another story.
Test automation process model to evaluate
Before making any calculations we should define the model we should work with. At the moment we'll take simple model when test automation is used for the purpose of minimizing regression testing efforts. Thus we have:
- Manual testing team which is responsible for test design/maintenance and test execution
- Test automation team which is responsible for automated tests development and maintenance
Additional assumptions:
- Automation team works only on existing tests automation and the only influence on manual team is reflected in minimized number of tests to execute manually
- Both manual and automation teams work iteratively. During each iteration they develop some tests, maintain existing tests and perform test execution
- Automated test execution doesn't impact the test automation team. It means that tests are executed either on nightly basis or on dedicated server so test automation engineers don't dedicate the time for test execution
- Existing tests maintenance and execution is of higher priority than new tests development. Thus, there will be the point when new development is impossible due to current workload on existing testing activities
- Iteration length is fixed and cannot be extended
- Team performance characteristics and team size is the same during all the time
- The testing environment is already available and no extra costs are needed to support it
Team constant costs structure
All the costs can be divided into:
- Constant costs - costs which are of one-time nature and do not depend on time spent
- Varying costs - costs which are changed with the time
Before calculating complex costs we should identify which costs are constant for each team.
Test Automation team
For the calculation purposes we'll use the following characteristics describing performance of test automation team:
- Tauto - the size of test automation team
- Wauto - the costs of hardware per test automation team member
- SWauto - the software costs per one test automation team member
- Sauto - the hourly salary for each test automation team member
- BEauto - the costs of test environment used for automation
- TPDauto - the hourly performance of each test automation team member (tests per hour)
- TMaintPDauto - the number of tests maintained per hour for one test automation team member
Those characteristics can be collected during the project. For now we assume those characteristics are fixed and do not change after the time. In reality it's a bit different but for current model that would be enough to have them fixed values.
The entire constant costs is the sum of software\hardware expences multiplied by team size. So, constant automation costs can be calculated using the formula:
Manual testing team
For the calculation purposes we'll use the following characteristics describing performance of manual testing team:
- Tman - the size of manual testing team
- Wman - the costs of hardrawe for manual testing team (including workstation and other auxiliary hardware costs)
- SWman - the costs for software used for manual testing (license costs)
- BEman - the costs for the testing environment (in this moel it's always 0 as we assume we already have an environment)
- Sman - hourly-based salary for each manual testing team member
- TPDman - the number of new tests produced by one manual tester during the hour
- AVGTIMEman - average time for single test execution for one manual tester
- TMaintPDman - the number of tests which are maintained by one manual tester per hour
All those characteristics can be collected as an average statistic information as well as some information (like salary) can be accessed.
As for automation team the constant costs for manual testing team can be represented with the following formula:
Test Automation team effort
Once we calculated the constant costs for test automation team let's see how both teams perform together in order to identify what the performance inprovement the test automation team brings to the testing process.
The total number of automated tests can be expressed using the following formula:
But this formula doesn't include the fact that some time should be spent on tests maintenance as well as we're limited with iteration length where we should be able both delivering new tests and maintain existing ones. So, the
TPDauto option becomes the function depending on time and iteration length. It can be represented with the following form:
The correlated tests pre hour coefficient is the function which linearly decreases as long as we add more tests. Graphically it looks like the following:
So, the entire formula is transformed to the function depending on time and Iteration length and has the following view:
So, the overall formula showing the number of developped tests becomes more complicated and it's behavior can be displayed with the following graph:
With the correlation coeficient the formula displaying the number of tests changed the meaning. Now it shows the number of automated tests which can be handled without breaking the iteration time lines. Thus, we have the dependency on iteration length. The longer iteration is the more tests we're capable to handle. If we make comparison between iteration length and tests number handled we can get the following comparison graph:
On one hand the longer iterations we make the more tests we can process but there's another side of this. The longer iterations we have the longer the testing cycle is and tests are executed with the less frequency. But that's a matter or separate measure. For now, we just should know that longer iterations extend the capacity of the team.
As it's seen from the graph there's some point of maximum after which the team performance stops growing. This is the point where the team capacity is overwhelmed and any further activities wouldn't bring the growth of the number of supported tests.
This point of time can be calculated. For this purpose we should differentiate the formula for total tests count and solve the following equation relatively unknown
t:
The solution of this equation is:
Thus, based on Iteration length and proportion between maintenance costs and development efforts we can identify the point where we reach maximum capacity for test automation team.
But in our model there's also manual test team and test automation team efforts are reflected in the manual test team productivity. Let's find out how then.
Manual Test team effort
The formula for manual tests looks similar to the formula for automation team:
The main difference is in the structure of correlated TPDman coeficient. Of course, we should include the efforts on maintenance. But also there's additional effort on test execution. That's why we reserve
AVGTIMEman metric indicating average time for single test execution. With the above parameters the correlated TPDman coeficient looks like:
But this formula doesn't include the test automation efforts. The more tests are automated they are excluded from the scope of manual testing. So, the total number of manual tests should be subtracted with the number of automated test. Final formula for correlated manual test team performance coeficient is:
Unlike the corresponding coeficient for automation team the
TPDmanCorr coeficient is more complex and non-linear as more factors are influencing on it. Graphically the correlated coeficient behaves in the following way:
That would impact of final graph behavior.
So, the final formula for the number of manual tests produced looks like the following:
Graphically that formula behaves in the following way:
Unlike the graph for test automation efforts this graph doesn't look so symmetrical. That's because additional test automation effort makes overall team performance coeficient non-linear.
All right, we have formulas to calculate the output from testing team. Now we are ready to calculate the benefits of test automation involvement.
ROI calculation
Identifying equivalent team sizes
We've expanded manual testing team with test automation team and got some progress in performance. But test automation isn't for free. We have to pay something for that. So, in order to find out the benefits from test automation we should find out how much it would take to reach the same performance but without test automation. Since we exclude such things as test descoping and iteration shifts the only measure we can move is the size of manual testing team. So, actually we should compare the efforts of manual + test automation team with the manual testing team which could show similar results.
First of all we should find out where we achieve the maximum capacity. On the previous graph that's the point of maximum. After that point we can't grow further. To calculate that maximum we should differentiate the formula for total tests count by
t variable and solve the following equation:
or "simplified" form:
The formula looks quite complex just due to big number of constants. But if we put the actual numbers the equation will be much simplier. E.g. I've set all the constants to some specific values and the equation starts looking like:
As it's seen from example we're getting just a quadratic equation which has 2 solutions. In general form they are calculated in the following way:
We're interested in the one where
t > 0 as our start time is 0. Let's name it as
Tmax and we'll refer to that value later as the time point where mixed manual and test automation team reaches the maximum.
OK. Now we know that our mixed team reaches the maximum after
t hours of work. Let's compare it with similar characteristics for team of manual testers only. We'll find use 2 measures:
- The manual testing team size which reaches the same tests count for the same time as the maximum for the mixed team. That would be upper bound.
- The manual testing team size which reaches the same maximum as the mixed team. That would be lower bound.
If we talk about team performance without test automation effort we'd use the same formula for manual testing but we should exclude the influence of test automation effort. So, the total number of tests at som point of time can be calculated with the following formula:
For current calculations the unknown variable here is
Team as we're looking for the team size performing with the same quality as mixed team.
So, let's find out how many manual testers are needed to reach the same maximum value and for the same time as it's needed for mixed team. For this purpose we'll take
Tmax as the value of
t and
TestsNoAuto value will be replaced with the value of
TotalManualCorr(Tmax,IterationLength). So, the equation looks like:
TotalManualCorr(Tmax, IterationLength) = TotalManualNoAuto(Tmax, IterationLength, Team)
I won't display result in general way as there're too many constants there. But the equation is linear and has only one solution.
So, now we know the number of people which can reach the maximum of mixed team during the same time. Let's name that value as
EqTeamSize1. Next measure is the team size which can show the same maximum. So, let's find the time when that maximum is reached first.
If we differentiate
TestsNoAuto function by
t we'll find out that the time when the maximum is reached doesn't depend on team size. The formula looks like:
The
TimeManMax value is the time when manual test team reaches the maximum. If we take the team without any automation the value doesn't depend on team size. It happens just because according to model the team is homogenous and all the activities are considered as parallel. So, the maximum point for single team member and entire team is the same. The only difference is with the number of the tests handled by that time. And if we put
TimeManMax value as the parameter to
TestsNoAuto we'll get the formula showing the maximal number of tests produced by such team. It looks like:
But at the same time we know how many tests are produced by mixed automation and manual team. So, we get an equation:
TotalManualCorr(Tmax, IterationLength) = TotalManualNoAuto(TimeManMax, IterationLength, Team)
Solving this equation we'll get the number of manual test engineers required to reach the same maximum number of tests handled. That would be the second measure we should collect. Lets name the value of such team size as
EqTeamSize2.
Calculating costs
Once we have the team sizes calculated we have everything to calculate the costs and their dependency on the time for all the teams.
Now we know all the parameters and we can describe the costs required both for mixed manual and automation team and their equivalent manual testing teams. The costs are calculated with the following formulas:
The clean profit can be identified as the difference between mixed team and equivalent teams costs. The formulas are:
These dependencies are linear so the main indicator showing that we're getting profit is that the following conditions are true:
Sman*(EqTeamSize1-Tman) > Sauto * Tauto
Sman*(EqTeamSize2-Tman) > Sauto * Tauto
The value of constant costs just shifts the point when the costs for automation start paying off.
And eventually, we invested some money in order to get some profit. Actually the investment is the costs spent on automation team. So, in order to calculate the ROI we should divide the clean profit by the costs of automation. Thus we'll get the following formulas:
That's it. That's the way to identify if our investment to automation really brings value and when it bring the value. All that's left is to put real parameters and analyze whether expectations are met or not. We should always keep in mind that it's not enough just to become profitable. If the point when we become profitable is expected after some date (e.g. far after end of the project) then the investment won't start paying off yet and we're losing the money at the end.
Example
We've defined all necessary formulas and we've made description of all the behaviors. Now it's time to see how it works on practice. We'll specify the values in the input parameters, identify the equivalent team sizes and identify whether our automation is profitable or not.
Given:
- Test Automation team
- Tauto = 1 (we add 1 automation engineer to the team)
- Wauto = 1000;
- SWauto = 12000 (let's say we use some expencive software)
- Sauto = 60000/(8*(12*22)) (annual salary is considered at about 60K which is 1.5 bigger than for manual tester)
- BEauto = 0 (we consider no additional costs for testing infrastructure is needed)
- TPDauto = 8 (that's quite good performance)
- TMaintPDauto = 20 (not very good maintenance velocity taking into account that the number of produced tests per day is quite big)
- Manual Testing team
- Tman = 1 (testing team has initially 1 manual test engineer)
- Wman = 1000;
- SWman = 0;
- BEman = 0;
- Sman = 40000/(8*(12*22));
- TPDman = 1/4;
- AVGTIMEman = 1/2 (each test takes about 30 minutes to execute)
- TMaintPDman = 5;
Using formulas from this article we'll get the following:
- The maximum for the team will be achieved after 136.1611783 items of time and it is 127.4630878 tests
- To reach the same value for the same time we need 5.332892381 people effort (Equivalent team size 1) which is near 5 (we wouldn't split people into pieces).
- In order to achieve the same maximum we need the team effort of 4.461208073. Let's take 5 to be sure that we really reach that numbers
So, we've added 1 test automation engineer to the team and got the performance which is comparable to the performance of 4 people. Sounds promising.
Joint graph of the tests delivery looks like:
As it's seen from the picture the first equivalent team can process more tests but manual testing team grows slower with the tests. That's why more people needed to reach the same number within the same time frame.
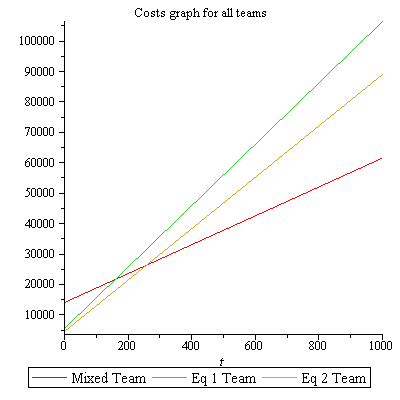
Having all necessary measures we can build graph representing the costs for all teams:
As it's seen from the graph the automation costs are initially greater than costs for manual testing team but the expences for mixed team are smaller. That's why the costs grow slower. So, after some time the expences on manual testing equivalent teams becomes bigger. That can be seem on the next graph representing the clean profit from automation effort:
Finally once we have the clean profit we can represent graph showing the ROI dynamics in time. It can be represented with the following graph:
With the team stuffing we provided we're getting 100% ROI in one year as a minimum just by the fact of adding 1 automation engineer with specified performance characteristics. Well, not so bad.
But that's just a model. Reality is much trickier and we have to manipulate different characteristics to make results better. But this math model at least helps to find out which parameters can be operated.
Conclusions
The math model described in this post is one of the simplest and a lot of parameters are simply fixed. The only things we could manipulate here is the team size and costs. But anyway, that model can make first approximation to see whether our automation is profitable or not as well as find the answae how profitable our automation is.
Of course, a lot of parameters are varying and the ability to shift them can give the possibility to increase the team capacity. Also, this model doesn't take into account the fact that test automation team may not have tests to automate (e.g. manual testers didn't prepare anything for them) and many other boundary conditions. But in further chapters I'll make the model more complicated including more varying factors to see how the model works and what corrective actions can be applied.


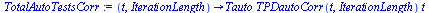























No comments:
Post a Comment